Jornal de Teoria Generalizada de Mentiras e Aplicações

Semi-Simplicity of a Lie Algebra of Isometries

Abstract

Anona Manelo

A spray S on the tangent bundle TM with a n dimensional differentiable manifold M defines an almost product structure Γ (Γ² =I, I being the identity vector 1-form) and decomposes the TTM space into a direct sum of horizontal space (corresponding to the eigenvalue +1) and vertical space (for the eigenvalue -1). The Lie algebra of projectable vector fields whose Lie derivative vanishes the spray S is of dimension at most n² +n. The elements of the algebra belonging to the horizontal nullity space of Nijenhuis tensor of Γ form a commutative ideal of . They are not the only ones for any spray S. If S is the canonical spray of a Riemannian manifold, the symplectic scalar 2-form Ω which is the generator of the spray S defines a Riemannian metric g upon the bundle vertical space of TM. The Lie algebra of infinitesimal isometries which is written 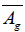contained in is of dimension at most 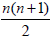. The commutative ideal of is also that of . 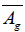The Lie algebra 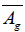of dimension superior or equal to three is semi-simple if and only if the nullity horizontal space of the Γ Nijenhuis tensor is reduced to zero. In this case, Ag is identical to . Mathematics Subject Classification (2010) 53XX • 17B66 • 53C08 • 53B05ns.