Jornal de Teoria Generalizada de Mentiras e Aplicações

Constructive Approach to Three Dimensional Sklyanin Algebras

Abstract

Natalia Iyudu and Stanislav Shkarin

A three dimensional Sklyanin is the quadratic algebra over a field 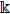with 3 generators x; y; z given by 3 relations xy - ayx - szz = 0, yz - azy - sxx = 0 and zx - axz - syy = 0, where a,s ∈ 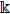. A generalized Sklyanin algebra is the algebra given by relations xy - a₁yx - s₁zz = 0, yz - a₂zy - s₂xx = 0 and zx - a₃xz - s₃yy = 0, where a_i, s_i∈ 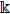. In this paper we announce the following results; the complete proofs will appear elsewhere. We determine explicitly the parameters for which these algebras has the same Hilbert series as the algebra of commutative polynomials in 3 indeterminates as well as when these algebras are Koszul and PBW, using constructive combinatorial methods. These provide new direct proofs of results established first by Artin, Tate, and Van Den Bergh.