Jianxin Zhu* and Luying Li
In this paper, for a class of complex optical waveguide, the high-precision computation of the propagation constants β are studied. The corresponding Sturm-Liouville (S-L) problem is represented as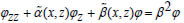 
in an open domain (open on one side), where x is a given value. Firstly, a perfectly matched layer is used
to terminate the open domain. Secondly, both the equation and the complex coordinate stretching transformations are constructed. Thirdly, the S-L problem is turned to a simplified form such as 
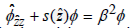in a bounded domain. Finally, the coefficient function 
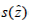is approximated by a piecewise polynomial of degree two. Since the simplified equation in each layer can be solved analytically by the Kummer functions, the approximate dispersion equation is established to the TE case. When the coefficient function is continuous, the approximate solutions converge fast to the exact ones, as the maximum value of the subinterval sizes tends to zero. Numerical simulations show that high-precision eigenmodes may be obtained by the Müller's method with suitable initial values.
Compartilhe este artigo
English 
Spanish 
Chinese 
Russian 
German 
French 
Japanese 
Hindi 